Pay Equity Deep Dive Part II: Wage Influencing Factors and Reliability Testing

![]()
This is Part II of our “Pay Equity Deep Dive Series.” Part I focused on Compensation Philosophy Review and Pay Analysis Group formation and testing. Part II focuses on Wage Influencing Factors (WIFs) and Reliability and Robustness Testing.
A Wage Influencing Factor (WIF) is a factor reflecting skill, effort, responsibility, working conditions, or location applied consistently in determining employees’ compensation.
Essentially, these are compensable factors that one would expect to influence employee pay. Examples include career level, job function/family, performance rating, company tenure, position tenure, line of business, educational attainment, and geographic location.
The Role Wage Influencing Factors Play in a Pay Equity Review
In our first deep dive, we defined the raw pay gap and decomposed it into explained and unexplained gaps. The graphic below is an illustrative example of these pay gaps. In this hypothetical example, the raw pay gap between men and women is $20,000 or 20%. The explained pay gap ($15,000) is the primary driver of the raw gap, with a smaller part ($5,000) left unexplained. Closing this unexplained pay inequity may require remedial adjustments in compensation.

To measure the part of the raw pay gap that cannot be explained and may be due to pay inequities, we need to measure the part of the raw pay gap that can be explained by legitimate, compensable factors (i.e., WIFs). We do this by using multiple regression.
Multiple regression estimates the relationship between an outcome, such as compensation, and multiple factors that are related to that outcome. Starting with compensation as our outcome of interest, we add relevant WIFs to a regression model. Once these WIFs are accounted for, we determine if gender, race/ethnicity, and other protected characteristics are statistically related to compensation. If so, we’ll put in place a remediation strategy to address these pay inequities.
How Do I Know What WIFs to Include in My Pay Models?
The WIF identification process begins with your compensation philosophy. Ask yourself, broadly speaking, what are the factors that your organization values and rewards? For example, if your organization has a pay-for-performance philosophy, then you’ll want to include performance in your pay models. Other “usual suspects” include company tenure, position tenure, and relevant experience prior to joining the organization.
Your pay models likely need to account for pay differences due to the nature of work (e.g., job, job family). Level of responsibility (e.g., individual contributor vs. manager vs. director) is also an important consideration. Geographic differentials are a relevant WIF for organizations that pay differently based on location. For some organizations, educational attainment and credentials impact compensation.
Once you’ve developed your list of potential WIFs, you’ll want to think about the extent to which these WIFs are relevant for all parts of your organization or only some. For example, educational attainment and credentials may be highly relevant in certain jobs or functions, but not relevant in others. We recommend creating a WIF matrix to help you think this through.
What Is a WIF Matrix?
A WIF matrix is a device to catalog which of the potential WIFs you identified are relevant for which parts of your organization. In the illustration below, we’ve catalogued WIFs by function for a prototypical technology company. For each function, we’ve noted whether a WIF is not relevant, relevant, or highly relevant.
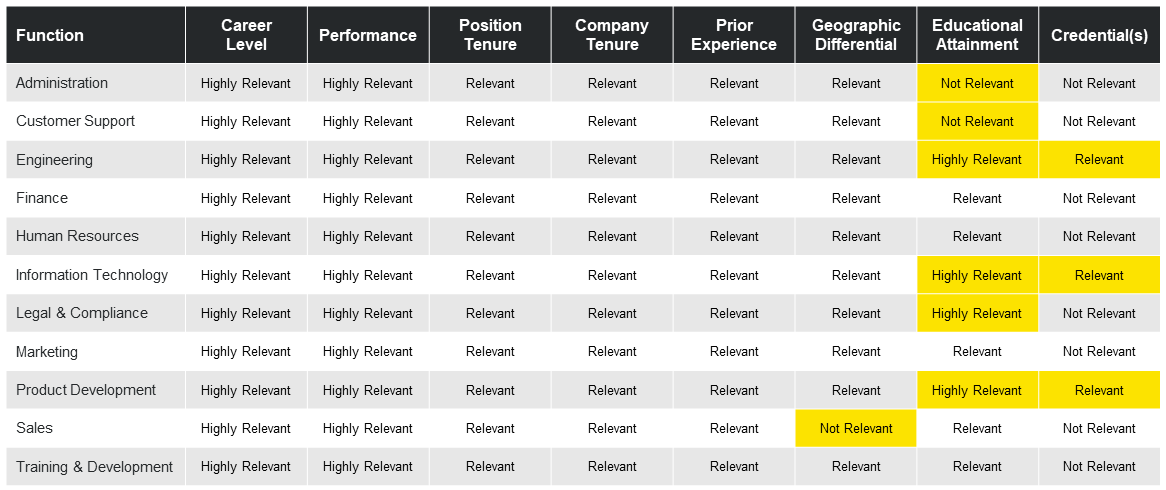
You’ll note that for this prototypical technology company, there is consistency in the relevancy of the WIFs across functions for Career Level, Performance, Position Tenure, Company Tenure, and Prior Experience. The yellow highlighting indicates cases in which the relevancy of the WIF is outside of the norm for the organization. In particular, there are no geographic differentials in Sales, so we list the factor as not relevant.
Moreover, Educational Attainment is not relevant in Administration and Customer Support. It is highly relevant in Engineering, Information Technology, Product Development, and Legal & Compliance. Credentials are only relevant in Engineering, Information Technology, and Product Development.
There is no need to use “Function” when creating your WIF matrix. We’ve seen organizations use the same relevancy weights across their entire workforce. Others have identified differences at the job level. We suggest starting this exercise with a “top down” approach. Are there broad segments of your workforce for whom all the WIFs have the same or mostly the same relevancy? Start there, and then work “bottoms up” to make refinements where applicable.
I’ve Created a WIF Matrix, Now What?
The next question to ask is whether structured data is available for the relevant factors in your WIF matrix. For example, it’s common for companies to use educational attainment and credential information in setting pay for new hires. Whether a company collects this information in a structured database is another question. If it does, is the information updated for employees that advance their education or obtain credentials after hire?
Prior Experience is another WIF that companies often use in setting pay for new hires. While many companies now collect this information electronically (during the application process), it’s likely available only for more recent hires. Lastly, we’ve also seen some organizations move away from performance ratings. We won’t comment on whether this is a good idea, but it will make it more difficult to account for performance as a WIF in your pay equity analysis.
What if I Don’t Have Structured Data on All of My WIFs?
All hope is not lost if you don’t have structured data on WIFs you noted as relevant or highly relevant. For Educational Attainment and Credentials, we suggest putting in place a plan to begin collecting this information. The most important places to start are the workforce segments where these WIFs are highly relevant. It will take time to collect this information. You’ll be laying the foundation for a more robust pay equity process in the future. You may want to do the same for Prior Work Experience. In the meantime, it’s customary to use employee age to create a proxy for prior work experience (e.g., Age – Company Tenure – 21).
If your organization does not have performance ratings, then you’ll want to incorporate performance into your remediation process. As you review employees flagged for a possible pay adjustment, confer with each employee’s manager to determine if there is a performance issue that explains the employee’s pay situation and whether a pay adjustment is warranted.
WIF Selection
Once you’ve completed your WIF matrix and created your Pay Analysis Groups (PAGs), you’re ready to develop your pay models. Assuming your focus is base pay, you’ll develop a model of base pay for each PAG. Use the WIF matrix to help you select the WIFs to include in each model. As an example, let’s suppose that our PAGs are the Functions included in the WIF matrix above. Further, suppose that we have data on Performance and Educational Attainment, but no data on Credentials or Prior Experience. We will use age to create a proxy for prior experience. Here is what our initial models look like for each of the eleven functions:
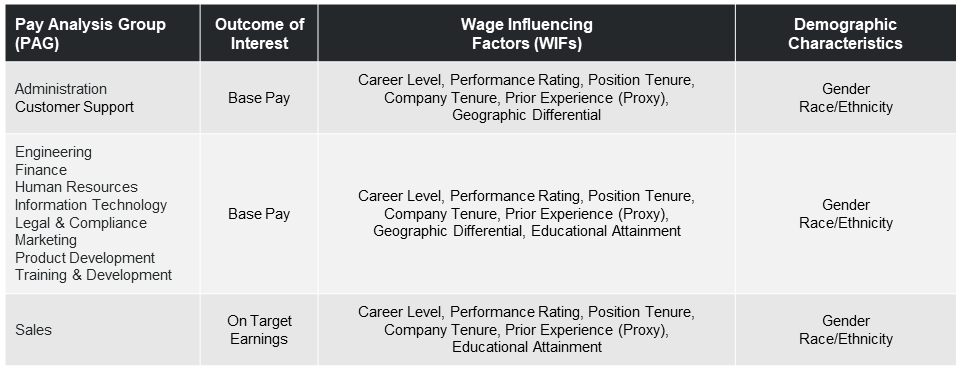
Note that the Administration and Customer Support models exclude Educational Attainment. The Sales model excludes Geographic Differentials. Also note that the outcome of interest for the Sales function is on-target earnings (OTE) in place of base pay.
WIF Consolidation & Refinement
We recommend the following best practices to consolidate and refine the WIFs included in your models.
1. For each categorical WIF in your model, each category value should have at least five employees.
Categorical WIFs are those in which the values are categories. In our example above, let’s assume Performance Rating consists of the following five values:
- Fails to meet expectations
- Partially meets expectations
- Meets expectations
- Exceeds expectations
- Far exceeds expectations
For some of the PAGs, fewer than five employees have a rating of “Fails to meet expectations.” In these cases, we can consider combining the lowest two ratings— “Fails to meet expectations” and “Partially meets expectations”—into a new category that we’ll call “below expectations.” Assuming this new category has at least five employees, we can use this alternative version as needed in our models.
2. Be mindful of low-incumbent job titles.
You’ll note that we have not included Job Title as a WIF in our example above. Your job titles can be used as WIFs if they meet the minimum incumbency condition outlined in No. 1. Including a job title with fewer than five employees as a WIF in a model can lead to unreliable results.
3. Aim for a model adjusted R-squared of at least 70%.
The purpose of the models we are creating is to explain the observed variation in pay within each PAG using the WIFs we have included, plus demographic characteristics. Ideally, we’d like these factors to explain at least 70% of the variation in pay in the PAG. This translates into a model adjusted R-squared of 70%.
4. Ensure the ratio of the number of employees in a PAG to the number of WIFs is at least five.
For each model, compute the ratio between the number of employees in a PAG and the number of WIFs. Note that categorical WIFs have multiple values. Each value counts as a separate WIF in this calculation. Take the Administration model as an example. Assume that Career Level has six values, Performance Rating has five values, and Geographic Differential has three values. Position Tenure, Company Tenure, and Prior Experience (Proxy) each count as one in this calculation. The total number of WIFs in the Administration model is seventeen. To ensure we have at least five employees per WIF, Administration would need to have at least 85 employees.
5. At least 70% of the WIFs in the model should be statistically significant.
Including too many statistically insignificant WIFs can create unreliable results and runs the risk of mismeasuring pay disparities. Our recommended rule of thumb is that 70% of the WIFs in a model should be statistically significant. If you find that your models do not meet this condition, we recommend pruning your model. For example, if none of the performance rating values are statistically significant, consider removing these WIFs from the model.
Reliability and Robustness Testing
When conducting a pay equity review, a primary aim is to determine if, based on the regression results, we see any pay disparities that appear to be related to gender, race/ethnicity, or another demographic characteristic. The statistical significance of a pay disparity is typically measured using a 5% significance level (i.e., p-value ≤ 0.05). This is a commonly used significance threshold. It indicates that the result we are seeing is unlikely to be due to chance and is statistically meaningful.
In PAGs in which we see statistically significant pay disparities, we may want to make remedial pay adjustments. However, just because a pay disparity is statistically significant does not mean that it is sufficiently reliable as a basis for making pay adjustments. Conversely, just because a pay disparity is not statistically significant does not mean it can be safely ignored.
We have developed a set of criteria to identify whether modeling results for a given PAG are reliable and robust.
Reliability Tests:
- Adjusted R-squared of model is at least 70%.
- Ratio of number of employees to number of WIFs is at least five.
- Proportion of WIFs that are statistically significant is at least 70%.
Robustness Tests:
- For statistically significant pay disparities, a meaningful pay disparity remains when statistically insignificant WIFs are added to the model.
- For statistically significant pay disparities, a meaningful pay disparity remains when influential observations are dropped from the model.
- Statistically insignificant pay disparities remain below a 10% level of statistical significance under both of the preceding exercises. Note that pay disparities significant at a 10% level of statistical significance are automatically classified as not reliable.
What if My Models Do Not Pass Reliability and Robustness Tests?
Here are some steps you can take if your models fail one or more of the reliability and robustness tests:

We do not recommend engaging in remediation efforts in PAGs that do not pass these reliability and robustness tests.
* * * * * *
Stay tuned for Part III of our “Pay Equity Deep-Dive” series, which will cover Tainted Variable Analysis and Root Cause Assessment.